Scan Converting a Straight Line
Scan converting a straight line is the process of determining the set of pixels or points on a display or image that lie along a straight line segment. This technique is commonly used in computer graphics and is essential for rendering lines and other geometric primitives. In the fig given below the two endpoints are described by (x1,y1) & (x2,y2).
Equation of the straight line
To define a straight line we use the following equation.
y= mx + a
Where,
(x, y) = axis.
m = Slope of the line.
a = Interception point

According to the equation of a straight line, y = mx + b where m = 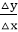 and b = the y interrupt, we can find values of y by incrementing x from x =x1 to x = x2. By scan-converting these calculated x, and y values, we represent the line as a sequence of pixels.
and b = the y interrupt, we can find values of y by incrementing x from x =x1 to x = x2. By scan-converting these calculated x, and y values, we represent the line as a sequence of pixels.
Properties of Good Line Drawing Algorithm:
Following properties of a good Line Drawing Algorithm.
- An algorithm should be precise: Each step of the algorithm must be adequately defined.
- Finiteness: An algorithm must contain finiteness. It means the algorithm stops after the execution of all steps.
- Easy to understand: An algorithm must learners to understand the solution in a more natural way.
- Correctness: The algorithm must be in the correct manner.
- Effectiveness: All steps of an algorithm must be valid and efficient.
- Uniqueness: All steps should be clearly and uniquely defined, and the result should be based on the given input.
- Input: The algorithm must accept at least one or more inputs.
- Output: At least one out must be generated by the algorithm.
Algorithm for line Drawing:
There are the following algorithms used for drawing a line:
- DDA (Digital Differential Analyzer) Line Drawing Algorithm
- Bresenham’s Line Drawing Algorithm
- Mid-Point Line Drawing Algorithm
Related Articles


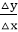 and b = the y interrupt, we can find values of y by incrementing x from x =x1 to x = x2. By scan-converting these calculated x, and y values, we represent the line as a sequence of pixels.
and b = the y interrupt, we can find values of y by incrementing x from x =x1 to x = x2. By scan-converting these calculated x, and y values, we represent the line as a sequence of pixels.