Scan conversion in computer graphics refers to the process of converting geometric primitives, such as lines, curves, or polygons, into a rasterized form for display on a pixel-based screen. It involves determining which pixels should be illuminated or assigned specific attributes to accurately represent the desired shapes and objects. Scan conversion enables efficient rendering and precise control over individual pixels, forming the basis for generating graphics on modern digital displays.
Methods of Scan Conversion in computer graphics
Mostly we perform scan conversion in computer graphics by using two methods Analog Method and Digital Method.
It is the best method for analog videos. A large number of delay cells perform the analog method. The Analog approach is also known as the “Non-retentive, memory-less, or real-time method.”
The digital method is also known as a “retentive or buffered method.” In the digital method, there is a concept of n1 and n2 speed. We can save (Store) the picture in line or frame buffer with n1 speed. The image can be read with n2 speed.
Some Examples of scan-converted objects
We can apply the conversion to the following objects.
- Line
- Point
- Polygon
- Rectangle
- Filled Region
- Arc
- Character
- Sector
- Ellipse
Pixel or Pel:
In computer graphics, the terms "pixel" and "pel" are often used interchangeably to refer to the smallest unit of a digital image or display. Both terms are derived from "picture element" and essentially represent the same concept.
A pixel includes its own:
- Intensity – The intensity of a pixel defines the brightness of the image that appears on the screen.
- Name or Address- The name or address of a pixel defines the position of the pixel.
We can define the size of any image with a total number of horizontal pixels and the total number of vertical pixels.
For Example- (1024 x 768, 640x480 or 512 x 512).
We can measure the ratio of an image's width to its height in unit length or number of pixels, which is known as the aspect ratio of the image.
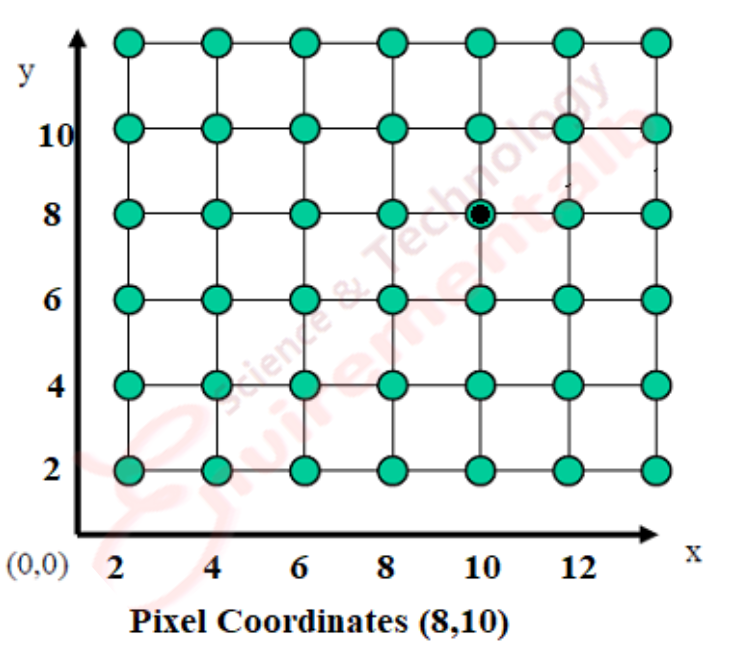
For example- A Pixel has a coordinate (8,10).
Example of Pixel
Advantages of Scan Conversion
Scan conversion, also known as rasterization, offers several advantages in computer graphics. Here are some of the key advantages:
- Efficient rendering of complex scenes in real-time.
- Precise control over individual pixels for detailed rendering.
- Versatile representation of different geometric primitives.
- Compatibility with various output devices and displays.
- Hardware acceleration for faster rendering speeds.
- Integration with other graphics techniques and algorithms.
- Accurate representation of shapes, textures, and lighting.
- Enables interactive graphics applications like gaming and simulations.
- Provides a unified framework for rendering diverse graphical elements.
- Facilitates the creation of visually appealing and realistic graphics.
Disadvantages of Scan Conversion
Certainly! Here's a list of potential disadvantages or challenges associated with scan conversion in computer graphics:
- Scan conversion can result in aliasing artifacts, where smooth curves or diagonal lines appear jagged or pixelated. Anti-aliasing techniques are needed to mitigate this issue.
- Scan conversion involves approximating continuous geometric primitives with discrete pixels, leading to a loss of precision. This can result in inaccuracies and visual distortions, particularly for complex shapes or curves.
- Scan conversion algorithms can be computationally intensive, especially for rendering complex scenes or high-resolution displays. Real-time rendering of detailed scenes may require optimization techniques and efficient algorithms.
- Rasterizing geometric primitives into a pixel grid requires memory allocation for storing pixel attributes. This can lead to significant memory consumption, especially for high-resolution displays or scenes with a large number of primitives.
- Scan conversion algorithms may exhibit artifacts or incorrect rendering in certain edge cases or uncommon scenarios. Handling concave polygons, self-intersecting shapes, or complex curve geometries can pose challenges.
- Scan conversion techniques may face limitations in terms of handling extremely large or highly detailed scenes. Real-time rendering of such scenes may require advanced optimization techniques or simplified representations.
- Scan conversion relies on the resolution of the output device. Lower-resolution displays may exhibit pixelation or reduced visual quality, particularly when rendering fine details or small primitives.
- Achieving accurate shading and lighting effects solely through scan conversion can be challenging. Advanced shading models, such as ray tracing or global illumination, may be required for more realistic rendering.
- Scan conversion is primarily designed for pixel-based rendering. Representing non-pixel-based objects, such as vector graphics or mathematical curves, may require additional techniques or conversions.
Related Articles